Digital computers communicate with external devices through ports: sets of terminals usually arranged in groups of 4, 8, 16, or more (4 bits = 1 nybble, 8 bits = 1 byte, 16 bits = 2 bytes). These terminals may be set to high or low logic states by writing a program for the computer that sends a numerical value to the port. For example, here is an illustration of a micro controller being instructed to send the hexadecimal number F3 to port A and 2C to port B:

|
|
Suppose we wished to use the upper four bits of port A (pins 7, 6, 5, and 4) to drive the coils of a stepper motor in this eight-step sequence:
As each pin goes high, it drives a power MOSFET on, which sends current through that respective coil of the stepper motor. By following a “shift” sequence as shown, the motor will rotate a small amount for each cycle.
Write the necessary sequence of numbers to be sent to port A to generate this specific order of bit shifts, in hexadecimal. Leave the lower four bit of port A all in the low logic state.
Follow-up question: write the same sequence in decimal rather than hexadecimal:
Although the root of this question is nothing more than binary-to-hexadecimal conversion, it also introduces students to the concept of controlling bit states in microcomputer ports by writing hex values. As such, this question is very practical!
In case students ask, let them know that a dollar sign prefix is sometimes used to denote a hexadecimal number. Other times, the prefix 0x is used (e.g., $F3 and 0xF3 mean the same thing).
The numeration system we use in our daily lives is called base ten, also called decimal or denary. What, exactly, does “base ten” mean?
Given the following base-ten number, identify which digits occupy the “one’s place,” “ten’s place,” “hundred’s place,” and “thousand’s place,” respectively:
|
“Base ten” means that numbers are represented by combinations of symbols (ciphers), of which there are only ten (0, 1, 2, 3, 4, 5, 6, 7, 8, and 9).
Analyzing the number 5,183:
The “base” of our numeration system is something people usually don’t think much about - it is simply taken for granted. The purpose of this question is to help students realize what numerical symbols actually mean, in preparation for understanding other systems of numeration.
Observe the following sequence of numbers:
00
01
02
03
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
.
.
.
What pattern(s) do you notice in the digits, as we count upward from 0 to 21 (and beyond)? This may seem like a very simplistic question (and it is!), but it is important to recognize any inherent patterns so that you may understand counting sequences in numeration systems with bases other than ten.
Note the repeating sequence of digits in the one’s place, and the developing pattern of incrementation in the ten’s place. How many numbers may be counted without repeating digits in the one’s place?
Some students will think this question to be ridiculously simple, but there are some important lessons to be learned here. The greatest problem students face while learning binary, octal, and hexadecimal numeration systems is the overpowering familiarity with base-ten numeration. We are so accustomed to base-ten that we don’t bother to recognize its basic properties, and typically believe that this is the only way numbers may be written!
The ancient Mayans used a vigesimal, or base-twenty, numeration system in their mathematics. Each “digit” was a actually a composite of dots and/or lines, as such:
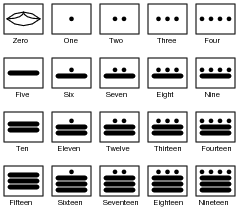
|
|
To represent numbers larger than twenty, the Mayans combined multiple “digits” the same way we do to represent numbers larger than ten. For example:
|
|
Based on the examples shown above, determine the place-weighting of each “digit” in the vigesimal numeration system. For example, in our denary, or base-ten, system, we have a one’s place, a ten’s place, a hundred’s place, and so on, each successive “place” having ten times the “weight” of the place before it. What are the values of the respective “places” in the Mayan system?
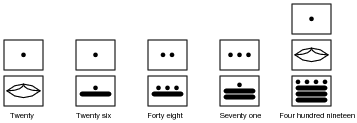
Also, determine the values of these Mayan numbers:

|
|
Place weights: one’s, twenty’s, four hundred’s, eight thousand’s, . . .

|
|
Although no one counts in “Mayan” anymore, this question is still relevant because it gets students thinking outside their accustomed numeration system. Also, it has some cultural value, showing them that not everyone in the world counts the same way they do!
Digital computers use a numeration system with a base of two, rather than a base of ten as we are accustomed to using. It is much easier to engineer circuitry that counts in “binary” than it is to design circuits that count in any other base system. Based on what you know of numeration systems, answer the following questions:
There are only two valid ciphers in the binary system: 0 and 1. Each successive place carries twice the “weight” of the one before it. Seventeen = 10001 (in binary). Each character in the binary system is called a “bit” rather than a “digit”.
Ask your students to hypothesize why binary is used in digital circuitry rather than base-ten (denary) numeration. I’ve revealed that it’s easier to build circuits representing quantities in binary than any other numerical base, but why?
If a digital meter display has four digits, it can represent any number from 0000 to 9999. This constitutes ten thousand unique numbers representable by the display. How many unique numbers could be represented by five digits? By six digits?
If an ancient Mayan ledger had spaces for writing numbers with three “digits” each, how many unique numbers could be represented in each space? What if the spaces were expanded to hold four “digits” each?
If a digital circuit has four bits, how many unique binary numbers can it represent? If we expanded its capabilities to eight bits, how many unique numbers could be represented by the circuit?
After answering these questions, do you see any mathematical pattern relating the number of “places” in a numeration system and the number of unique quantities that may be represented, given the “base” value (“radix”) of the numeration system? Write a mathematical expression that solves for the number of unique quantities representable, given the “base” of the system and the number of “places”.
Five denary digits: one hundred thousand unique numbers. Six denary digits: one million unique numbers.
Three vigesimal “digits”: eight thousand unique numbers. Four vigesimal “digits”: one hundred sixty thousand unique numbers.
Four binary bits: sixteen unique numbers. Eight binary bits: two hundred fifty six unique numbers.
|
Where,
b = Radix of numeration system.
n = Number of “places” given.
Ask your students which numeration system of the three given is more efficient in representing quantities with the smallest number of places. Then, ask them to explain why this is.
What is the largest number that can be counted to, in a base-ten system with six digits? How about in a base-twenty (vigesimal) system with four places? How about in a base-two (binary) system with ten bits?
99999910 = Nine hundred ninety nine thousand, nine hundred ninety nine.

|
|
11111111112 = one thousand twenty three.
Ask your students to explain why subscripts are desirable when writing numbers in binary, or in any other “base” numeration system for that matter.
How many binary bits are needed to count up to the number one million three hundred thousand seven hundred sixty two? Try to answer this question without converting this quantity into binary form, and then explain the mathematical procedure!
Twenty one bits.
Hint: the answer consists in solving this equation:
|
Where,
n = The number of binary bits necessary to count up to 1,300,762.
This question is a test of whether or not students know how to algebraically solve for variable exponents. I’m not going to suggest how this is done (lest I rob a student of the learning experience that comes from researching the answer on their own), but I will say that it is a very useful algebraic technique, once mastered.
If students still haven’t found a solution after doing their research, suggest they try to solve a simpler problem:
This question is trivial to answer (7 decimal digits), since we’re all familiar with decimal numeration. However, the real learning takes place when students write a mathematical expression for solving this problem, similar to the one written in the answer for the binary problem. Once they have that expression written, ask them what algebraic techniques could be used to solve for the exponent’s value.
The circuit shown in this diagram is used to transmit a numerical value from one location to another, by means of switches and lights:

|
|
Given the switches and lights shown, any whole number between 0 and 999 may be transmitted from the switch location to the light location.
In fact, the arrangement shown here is not too different from an obsolete design of electronic base-ten indicators known as Nixie tube displays, where each digit was represented by a neon-filled glass tube in which one of ten distinct electrodes (each in the shape of a digit, 0-9) could be energized, providing glowing numerals for a person to view.
However, the system shown in the above diagram is somewhat wasteful of wiring. If we were to use the same thirty-one conductor cable, we could represent a much broader range of numbers if each conductor represented a distinct binary bit, and we used binary rather than base-ten for the numeration system:

|
|
How many unique numbers are representable in this simple communications system? Also, what is the greatest individual number which may be sent from the “Sender” location to the “Receiver” location?
In this system, with a “width” of 30 bits, we are able to represent one billion, seventy three million, seven hundred forty one thousand, eight hundred twenty four unique numbers. The greatest individual number which may be communicated is one less than this total.
The purpose of this question is to allow students to consider an electric circuit that communicates digital quantities from one location to another, rather than abstractly discuss numeration systems. It also provides a more practical context in which to understand maximum count in a numeration system.
Explain why binary is a natural numeration system for expressing numbers in electronic circuits. Why not decimal or some other base of numeration?
How do you suspect binary numbers may be stored in electronic systems, for future retrieval? What advantages are there to the use of binary numeration in storage systems?
The two states of an on/off circuit are equivalent to 0 and 1 ciphers in binary. Any medium in which on/off states may be physically represented is applicable to storing binary numbers. Optical disks (CD-ROM, DVD) are an excellent example of this, with laser-burned “pits” representing binary bits.
Ask your students to think of different media or physical quantities which may represent binary information, especially those related to electric/electronic circuits.
Convert the following numbers from binary (base-two) to decimal (base-ten):
Describe a general, step-by-step procedure for converting binary numbers into decimal numbers.
The most important part of this question, of course, is the method of translating binary into decimal. Don’t tell your students how to do this, as there are plenty of good references to be found on the procedure. If a student cannot research and understand how to convert binary into decimal without your help, they aren’t trying hard enough!
Convert the following numbers from decimal (base-ten) to binary (base-two):
Describe a general, step-by-step procedure for converting decimal numbers into binary numbers.
The most important part of this question, of course, is the method of translating decimal into binary. Don’t tell your students how to do this, as there are plenty of good references to be found on the procedure. If a student cannot research and understand how to convert decimal into binary without your help, they aren’t trying hard enough!
A numeration system often used as a “shorthand” way of writing large binary numbers is the octal, or base-eight, system.
Based on what you know of place-weighted numeration systems, describe how many valid ciphers exist in the octal system, and the respective “weights” of each place in an octal number.
Also, perform the following conversions:
There are only eight valid ciphers in the octal system (0, 1, 2, 3, 4, 5, 6, and 7), with each successive place carrying eight times the “weight” of the place before it.
Follow-up question: why is octal considered a “shorthand” notation for binary numbers?
There are many references from which students may learn to perform these conversions. You assistance should be minimal, as these procedures are simple to comprehend and easy to find.
A numeration system often used as a “shorthand” way of writing large binary numbers is the hexadecimal, or base-sixteen, system.
Based on what you know of place-weighted numeration systems, describe how many valid ciphers exist in the hexadecimal system, and the respective “weights” of each place in a hexadecimal number.
Also, perform the following conversions:
There are sixteen valid ciphers in the hexadecimal system (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F), with each successive place carrying sixteen times the “weight” of the place before it.
Follow-up question: why is hexadecimal considered a “shorthand” notation for binary numbers?
There are many references from which students may learn to perform these conversions. You assistance should be minimal, as these procedures are simple to comprehend and easy to find.
Complete this table, performing all necessary conversions between numeration systems:

|
|

|
|
Lots of conversions to do here! I particularly like the “table” format shown here for practicing numeration system conversions, because it compresses a lot of practice into a small space on paper, and also because it allows students to use different methods of conversion. For example, in converting a decimal number to the other forms, a student might choose to convert first to binary, then from binary to octal and hex. Or, alternatively, a student may choose to convert from decimal into hex, then from hex into binary, then from binary to octal, the last two conversions being especially easy.
When representing non-whole numbers, we extend the “places” of our decimal numeration system past the right of the decimal point, like this:

|
|
How do you suppose we represent non-whole numbers in a numeration system with a base (or “radix”) other than ten? In the following examples, write the place-weight values underneath each place, and then determine the decimal equivalent of each example number:

|
|

|
|

|
|

|
|

|
|

|
|
Many students will not realize initially that it is possible to represent non-whole numbers in binary, octal, or hexadecimal. Really, though, the concept is identical to the representation of non-whole numbers in decimal form. The ability of your students to grasp non-whole numbers in these other numeration systems indicates their grasp of place-weighted systems in general. If a student truly comprehends how place-weighting works, they will have no trouble understanding digits to the left or the right of the radix point in any numeration system. If a student does not understand how digits to the right of the decimal point are interpreted in other numeration systems, then they need to spend more time reviewing what decimal numbers mean.
It’s not that the concept is so hard to understand, so much as it is our familiarity with the decimal (base-ten) numeration system. We grow so accustomed to one way of representing numbers that we don’t realize what the symbols actually mean, or that there may be alternative methods of representing quantities.
Convert the following numbers (all between the values of 0 and 1) into decimal form:
Ask your students to explain the method of conversion used in each case. It is rather simple, but important to understand nonetheless. Ask your students how this method compares with the conversion of whole-number values into decimal form.
Complete this table, performing all necessary conversions between numeration systems. Truncate all answers to three characters past the point:

|
|

|
|
Lots of conversions to do here! I particularly like the “table” format shown here for practicing numeration system conversions, because it compresses a lot of practice into a small space on paper, and also because it allows students to use different methods of conversion. For example, in converting a decimal number to the other forms, a student might choose to convert first to binary, then from binary to octal and hex. Or, alternatively, a student may choose to convert from decimal into hex, then from hex into binary, then from binary to octal, the last two conversions being especially easy.
In digital computer systems, binary numbers are often represented by a fixed number of bits, such as 8, or 16, or 32. Such bit groupings are often given special names, because they are so common in digital systems:
How many binary bits is represented by each of the above terms?
And, for those looking for more challenge, try defining these terms:
The term “word,” is often used to represent 16 bits, but it really depends on the particular system being spoken of. A binary “word” is more accurately defined as the default width of a binary bit grouping in a digital system.
Follow-up question: what binary grouping corresponds to a single hexadecimal character?
Definitions taken from The New Hacker’s Dictionary, available on internet terminals everywhere.
Published under the terms and conditions of the Creative Commons Attribution License

In Partnership with Sager Electronics

by Aaron Carman


by Duane Benson
