Define the following terms: energy, work, and power.
Work is the exertion of a force over a distance. Energy is the capacity to perform work. Power is the rate of work performed per unit time.
Students may find a basic physics text helpful in obtaining these definitions. “Work” is a difficult concept to precisely define, especially for students unfamiliar with basic physics. Technically, it is the vector dot-product of force and displacement, meaning that work equals force times distance only if the force and distance vectors are precisely parallel to each other. In other words, if I carry a 10 kg mass (lifting up against the tug of gravity) while walking parallel to the ground (not going up or down), the force and displacement vectors are perpendicular to each other, and the work I do in carrying the mass is zero. It is only if my force is directed precisely the same direction as my motion that all of my effort is translated into work.
Voltage is commonly defined as “electrical pressure.” The unit of the volt, however, may be defined in terms of more fundamental physical units. What are these units, and how do they relate to the unit of the volt?
1 volt is equal to 1 joule of energy imparted to 1 coulomb of charge (6.25 ×1018 electrons):
$$V= \frac {W}{Q}$$
Where,
V = Voltage (volts)
W = Work, or potential energy (joules)
Q = Charge (coulombs)
Note that I use the letter “V” to denote voltage rather than “E” as I usually do. This is because in general physics work, “E” usually stands for either “Energy” or “Electric field”. Some electronics reference books use the letter “E” for voltage, while others use the letter “V”, or even use the two letters interchangeably.
Electric current is measured in the unit of the ampere, or amp. What is the physical definition for this unit? What fundamental quantities constitute 1 ampere of electric current?
1 ampere of electric current is the rate of electron motion equal to 1 coulomb per second:
$$I= \frac {Q}{t}$$
Where,
I = Electric current (amperes)
Q = Charge in motion (coulombs)
t = Time (seconds)
It may be helpful at this point to review the number of electrons constituting one coulomb of charge: 6.25 ×1018 electrons.
Technically, current’s mathematical definition involves calculus:
$$I= \frac {dQ}{dt}$$
However, students at this stage may not be ready to explore derivatives yet, and so the equation give in the answer for (average) current will suffice.
For a given amount of water pressure, which will flow a greater rate of water: a small (restrictive) nozzle or a large (unrestrictive) nozzle? Explain how this relates to the study of voltage, current, and resistance in a simple electric circuit.

| |
Obviously, an unrestrictive nozzle will pass a greater flow rate of water through it, all other factors being equal. In an electric circuit, less resistance will pass a greater flow rate of electrons (current) for a given amount of “pressure” (voltage).
Water flow is not a perfect analogy for electricity, but is close enough to be useful in basic electricity education. Be prepared to discuss the inadequacies of water as an analogy with your students (i.e. “How come electrons don’t spill out the end of an open wire like water spills out the end of an open hose or pipe?”).
Suppose you were to build this circuit and take measurements of current through the resistor and voltage across the resistor:

| |
Recording these numerical values in a table, the results look something like this:
| XXXXXXX | XXXXXXX |
| Current | Voltage |
| 0.22 A | 0.66 V |
| 0.47 A | 1.42 V |
| 0.85 A | 2.54 V |
| 1.05 A | 3.16 V |
| 1.50 A | 4.51 V |
| 1.80 A | 5.41 V |
| 2.00 A | 5.99 V |
| 2.51 A | 7.49 V |
Plot these figures on the following graph:

| |
What mathematical relationship do you see between voltage and current in this simple circuit?
This is an example of a linear function: where the plot describing the data set traces a straight line on a graph. From this line, and also from the numerical figures, you should be able to discern a constant ratio between voltage and current.
The raw data figures were made intentionally “noisy” in this problem to simulate the types of measurement errors encountered in real life. One tool which helps overcome interpretational problems resulting from noise like this is graphing. Even with noise present, the linearity of the function is quite clearly revealed.
Your students should learn to make graphs as tools for their own understanding of data. When relationships between numbers are represented in graphical form, it lends another mode of expression to the data, helping people to apprehend patterns easier than by reviewing rows and columns of numbers.
Explain, step by step, how to calculate the amount of current (I) that will go through the resistor in this circuit:

| |
Resistor current = 0.02553 amps, or 25.53 milliamps (mA).
Just a simple Ohm’s Law calculation here - no tricks! The point of this question, however, is to get students to think about the steps they follow in doing the calculation. Many students simply wish to memorize procedures rather than learn why to do what they need to do to answer such questions. It is your task as the instructor to challenge them beyond memorization, and through to understanding.
|
Plot the relationships between voltage and current for resistors of three different values (1 Ω, 2 Ω, and 3 Ω), all on the same graph:

| |
What pattern do you see represented by your three plots? What relationship is there between the amount of resistance and the nature of the voltage/current function as it appears on the graph?
Advanced question: in calculus, the instantaneous rate-of-change of an (x,y) function is expressed through the use of the derivative notation: [dy/dx]. How would the derivative for each of these three plots be properly expressed using calculus notation? Explain how the derivatives of these functions relate to real electrical quantities.
The greater the resistance, the steeper the slope of the plotted line.
Advanced answer: the proper way to express the derivative of each of these plots is [dv/di]. The derivative of a linear function is a constant, and in each of these three cases that constant equals the resistor resistance in ohms. So, we could say that for simple resistor circuits, the instantaneous rate-of-change for a voltage/current function is the resistance of the circuit.
Students need to become comfortable with graphs, and creating their own simple graphs is an excellent way to develop this understanding. A graphical representation of the Ohm’s Law function allows students another “view” of the concept, allowing them to more easily understand more advanced concepts such as negative resistance.
If students have access to either a graphing calculator or computer software capable of drawing 2-dimensional graphs, encourage them to plot the functions using these technological resources.
I have found it a good habit to “sneak” mathematical concepts into physical science courses whenever possible. For so many people, math is an abstract and confusing subject, which may be understood only in the context of real-life application. The studies of electricity and electronics are rich in mathematical context, so exploit it whenever possible! Your students will greatly benefit.
What is the value of this resistor, in ohms (Ω)?

| |
Resistor value = 2700 Ω, or 2.7 kΩ.
One format of component value expression popular in Europe is to replace the decimal point with the metric prefix, so 2.7 kΩ would be represented as 2k7 Ω. Not only is this notation simpler, but it also transcends the interpretational difficulties experienced between Europeans and Americans with their opposite usages of commas and decimal points.
Some students might not realize that in Europe, commas are used as decimal points and visa-versa. Thus, two thousand seven hundred would be written as 2,700 in America and 2.700 in Europe. Conversely, the number π would be written as 3.141593 in America but 3,141593 in Europe. Confusing? Yes!!
A common saying about electricity is that it always takes the path of least resistance.” Explain how this proverb relates to the following circuit, where electric current from the battery encounters two alternate paths, one being less resistive than the other:

| |
The 250 Ω resistor will experience a current of 40 mA, while the 800 Ω resistor will experience a current of 12.5 mA.
As an instructor, I was very surprised to hear many beginning students claim that all current would go through the lesser resistor, and none through the greater resistor! The proverb about “takes the path of least resistance” really should be understood as “proportionately taking paths of lesser resistance.” People new to the study of electricity often misunderstand such basic principles, their errors usually based on folk wisdom like this. It is imperative to break through these myths with hard fact. In this case, Ohm’s Law serves as a mathematical tool we can use to dispel false ideas.
Of course, a circuit as simple as this may be readily assembled and tested in class, so that all may see the truth for themselves.
One style of light bulb, very different from the “incandescent” design which works on the principle of a super-heated wire filament emitting light, is called a gas discharge tube. In this design of light bulb, light is produced by the direct “excitation” of gas molecules as electric current passes between two electrodes:

| |
Both types of light bulbs have interesting voltage/current plots, neither one being identical to the voltage/current plot of a resistor. First, the voltage/current plot for an incandescent light bulb:
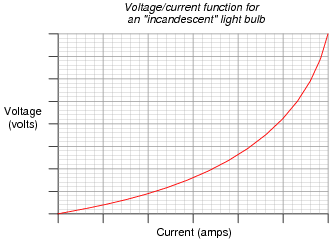
| |
Next, the voltage/current plot for a gas-discharge light bulb:

| |
Based on these two graphs, what can you say about the electrical resistance of each bulb type over its operating range?
Unlike a resistor, which offers a relatively fixed (unchanging) amount of resistance to the motion of electrons over a wide range of operating conditions, the electrical resistance of light bulbs typically change dramatically over their respective operating ranges.
From the graphs, determine where the resistance for each type of light bulb is at its maximum, and where the resistance is at its minimum.
Many types of electrical and electronic components experience changes in electrical resistance over their operating ranges of current and voltage. Resistors, while simple to study, do not exhibit the behavior of most electronic components. It is important for students to understand that the real world of electricity and electronics is much more complex than what Ohm’s Law might suggest (with an implicit assumption of fixed resistance). This is one concept that graphs really help to illustrate.
Draw the schematic diagram for an experimental circuit to gather data necessary to plot the voltage/current graph of a gas discharge lamp.

| |
One of my goals as a technical educator is to encourage the development of experimentation skills in my students. The most accurate way to gain knowledge of a device’s operation or of an electrical principle is to build a circuit that actually tests it. I’ve used this technique many times in my career to further my knowledge on a subject, and it has proven to be an invaluable skill.
In this question, students are implicitly asked to identify several key things:
Additionally, the students must identify what voltage/current ranges will be necessary to test a gas-discharge lamp. Notice the high-voltage power source shown in the schematic diagram. Students may ask “How high must this voltage be?” upon seeing the schematic in the answer. Don’t tell them outright. Rather, have them do some research and report the next day on typical lamp voltages!
What is negative resistance?
“Negative resistance” is where an electrical component passes less current as the voltage dropped across it increases.
Not only do many gas-discharge devices exhibit negative resistance over certain portions of their operating range, but many semiconductor devices do as well.
When an electric current passes through a conductor offering some electrical resistance, the temperature of that conductor increases above ambient. Why is this? Of what practical importance is this effect?
Electrical resistance is analogous to mechanical friction: electrons cannot freely flow through a resistance, and the “friction” they encounter translates some of their energy into heat, just as the friction in a worn mechanical bearing translates some of the kinetic energy of it’s rotation into heat, or the friction between a person’s hands while rubbing them together on a cold day translates some of the motion into heat.
This is a good starting point for a discussion on work, energy, and power. Power, of course, may be directly calculated by multiplying voltage by current, and is measured in watts. It also provides an opportunity to discuss some of the practical limitations of electrical conductors.
For a given amount of electric current, which resistor will dissipate the greatest amount of power: a small value (low-resistance) resistor, or a high value (high-resistance) resistor? Explain your answer.
A resistor with a high resistance rating (many “ohms” of resistance) will dissipate more heat power than a lower-valued resistor, given the same amount of electric current through it.
This question is designed to make students think qualitatively about the relationship between current, resistance, and power. I have found that qualitative (non-numeric) analysis is often more challenging than asking students to calculate answers quantitatively (with numbers). Often, simple math is a kind of barrier behind which students seek refuge from true understanding of a topic. In other words, it is easier to punch keys on a calculator (or even perform calculations with paper and pencil) than to really think about the inter-relationships of variables in a physical problem. Yet, a qualitative understanding of electrical systems is vital to fast and efficient troubleshooting.
Plot the relationship between power and current for a 2 Ω resistor on this graph:

| |
What pattern do you see represented by plot? How does this compare with the graphical relationship between voltage and current for a resistor?
The more current through the resistor, the more power dissipated. However, this is not a linear function!
Students need to become comfortable with graphs, and creating their own simple graphs is an excellent way to develop this understanding. A graphical representation of the Ohm’s Law (actually, Joule’s Law) power function allows students another “view” of the concept.
If students have access to either a graphing calculator or computer software capable of drawing 2-dimensional graphs, encourage them to plot the functions using these technological resources.
Shown here is a schematic diagram for a simple battery-powered flashlight:

| |
What could be modified about the circuit or its components to make the flashlight produce more light when turned on?
Somehow, the power dissipated by the light bulb must be increased. Perhaps the most obvious way to increase power dissipation is to use a battery with a greater voltage output, thus giving greater bulb current and greater power. However, this is not the only option! Think of another way the flashlight’s output may be increased.
The “obvious” solution is a direct application of Ohm’s Law. Other solutions may not be so direct, but they will all relate back to Ohm’s Law somehow.
There are two basic Ohm’s Law equations: one relating voltage, current, and resistance; and the other relating voltage, current, and power (the latter equation is sometimes known as Joule’s Law rather than Ohm’s Law):
$$E=IR$$
$$P=IE$$
In electronics textbooks and reference books, you will find twelve different variations of these two equations, one solving for each variable in terms of a unique pair of two other variables. However, you need not memorize all twelve equations if you have the ability to algebraically manipulate the two simple equations shown above.
Demonstrate how algebra is used to derive the ten “other” forms of the two Ohm’s Law / Joule’s Law equations shown here.
I won’t show you how to do the algebraic manipulations, but I will show you the ten other equations. First, those equations that may be derived strictly from \(E = IR\):
$$I= \frac {E}{R}$$
$$R= \frac {E}{I}$$
Next, those equations that may be derived strictly from \(P = I E\):
$$I= \frac {P}{E}$$
$$E= \frac {P}{I}$$
Next, those equations that may be derived by using algebraic substitution between the original two equations given in the question:
$$P=I^2R$$
$$P= \frac {E^2}{R}$$
And finally, those equations which may be derived from manipulating the last two power equations:
$$R= \frac {P}{I^2}$$
$$I=\sqrt{\frac{P}{R}}$$
$$E=\sqrt{PR}$$
$$R= \frac {E^2}{P}$$
Algebra is an extremely important tool in many technical fields. One nice thing about the study of electronics is that it provides a relatively simple context in which fundamental algebraic principles may be learned (or at least illuminated).
The same may be said for calculus concepts as well: basic principles of derivative and integral (with respect to time) may be easily applied to capacitor and inductor circuits, providing students with an accessible context in which these otherwise abstract concepts may be grasped. But calculus is a topic for later worksheet questions . . .
In this circuit, three resistors receive the same amount of current (4 amps) from a single source. Calculate the amount of voltage “dropped” by each resistor, as well as the amount of power dissipated by each resistor:

| |
E1 Ω = 4 volts
E2 Ω = 8 volts
E3 Ω = 12 volts
P1 Ω = 16 watts
P2 Ω = 32 watts
P3 Ω = 48 watts
Follow-up question: Compare the direction of current through all components in this circuit with the polarities of their respective voltage drops. What do you notice about the relationship between current direction and voltage polarity for the battery, versus for all the resistors? How does this relate to the identification of these components as either sources or loads?
The answers to this question should not create any surprises, especially when students understand electrical resistance in terms of friction: resistors with greater resistance (more friction to electron motion) require greater voltage (push) to get the same amount of current through them. Resistors with greater resistance (friction) will also dissipate more power in the form of heat, given the same amount of current.
Another purpose of this question is to instill in students’ minds the concept of components in a simple series circuit all sharing the same amount of current.
Challenge your students to recognize any mathematical patterns in the respective voltage drops and power dissipations. What can be said, mathematically, about the voltage drop across the 2 Ω resistor versus the 1 Ω resistor, for example?
In this circuit, three resistors receive the same amount of voltage (24 volts) from a single source. Calculate the amount of current “drawn” by each resistor, as well as the amount of power dissipated by each resistor:

| |
I1 Ω = 24 amps
I2 Ω = 12 amps
I3 Ω = 8 amps
P1 Ω = 576 watts
P2 Ω = 288 watts
P3 Ω = 192 watts
The answers to this question may seem paradoxical to students: the lowest value of resistor dissipates the greatest power. Math does not lie, though.
Another purpose of this question is to instill in students’ minds the concept of components in a simple parallel circuit all sharing the same amount of voltage.
Challenge your students to recognize any mathematical patterns in the respective currents and power dissipations. What can be said, mathematically, about the current drawn by the 2 Ω resistor versus the 1 Ω resistor, for example?
You might want to mention that in electrical parlance, a “heavy” load is one that draws a large amount of current, and thus has a large resistance. This circuit, which shows how the lowest resistance in a parallel circuit consumes the most power, gives practical support to the term “heavy” used to describe loads.
The brightness of a light bulb - or the power dissipated by any electrical load, for that matter - may be varied by inserting a variable resistance in the circuit, like this:

| |
This method of electrical power control is not without its disadvantages, though. Consider an example where the circuit current is 5 amps, the variable resistance is 2 Ω, and the lamp drops 20 volts of voltage across its terminals. Calculate the power dissipated by the lamp, the power dissipated by the variable resistance, and the total power provided by the voltage source. Then, explain why this method of power control is not ideal.
Plamp = 100 watts
Presistance = 50 watts
Ptotal = 150 watts
Follow-up question: note how in the original question I offered a set of hypothetical values to use in figuring out why a series rheostat (variable resistance) is not an efficient means to control lamp power. Explain how the assumption of certain values is a useful problem-solving technique in cases where no values are given to you.
Discuss the concept of energy conservation: that energy can neither be created nor destroyed, but merely changed between different forms. Based on this principle, the sum of all power dissipations in a circuit must equal the total amount of power supplied by the energy source, regardless of how the components are connected together.
A modern method of electrical power control involves inserting a fast-operating switch in-line with an electrical load, to switch power on and off to it very rapidly over time. Usually, a solid-state device such as a transistor is used:

| |
This circuit has been greatly simplified from that of a real, pulse-control power circuit. Just the transistor is shown (and not the “pulse” circuit which is needed to command it to turn on and off) for simplicity. All you need to be aware of is the fact that the transistor operates like a simple, single-pole single-throw (SPST) switch, except that it is controlled by an electrical current rather than by a mechanical force, and that it is able to switch on and off millions of times per second without wear or fatigue.
If the transistor is pulsed on and off fast enough, power to the light bulb may be varied as smoothly as if controlled by a variable resistor. However, there is very little energy wasted when using a fast-switching transistor to control electrical power, unlike when a variable resistance is used for the same task. This mode of electrical power control is commonly referred to as Pulse-Width Modulation, or PWM.
Explain why PWM power control is much more efficient than controlling load power by using a series resistance.
When the transistor is on, is acts like a closed switch: passing full load current, but dropping little voltage. Thus, its “ON” power \((P = I E)\) dissipation is minimal. Conversely, when the transistor is off, it acts like an open switch: passing no current at all. Thus, its “OFF” power dissipation \((P = I E)\) is zero. The power dissipated by the load (the light bulb) is the time-averaged power dissipated between “ON” and “OFF” transistor cycles. Thus, load power is controlled without “wasting” power across the control device.
Students may have a hard time grasping how a light bulb may be dimmed by turning it on and off really fast. The key to understanding this concept is to realize that the transistor’s switching time must be much faster than the time it takes for the light bulb’s filament to fully heat or fully cool. The situation is analogous to throttling the speed of an automobile by rapidly “pumping” the accelerator pedal. If done slowly, the result is a varying car speed. If done rapidly enough, though, the car’s mass averages the “ON”/“OFF” cycling of the pedal and results in a nearly steady speed.
This technique is very popular in industrial power control, and is gaining popularity as an audio amplification technique (known as Class D). The benefits of minimal wasted power by the control device are many.
What will happen to the brightness of the light bulb if the switch in this circuit is suddenly closed?

| |
Ideally, there will be no change whatsoever in the light bulb’s brightness when the switch is closed, because voltage sources are supposed to maintain constant voltage output regardless of loading. As you might have supposed, though, the additional current “drawn” by the resistor when the switch is closed might actually cause the lamp to dim slightly, due to the battery voltage “sagging” under the additional load. If the battery is well oversized for the application, though, the degree of voltage “sag” will be inconsequential.
This question illustrates a disparity between the ideal conditions generally assumed for theoretical calculations, and those conditions encountered in real life. Truly, it is the purpose of a voltage source to maintain a constant output voltage regardless of load (current drawn from it), but in real life this is nearly impossible. Most voltage sources exhibit some degree of “sag” in their output over a range of load currents, some worse than others.
In this example, it is impossible to tell how much the voltage source’s output will “sag” when the switch is closed, because we have no idea of what the resistor’s current draw will be compared to that of the light bulb, or what the voltage source’s rated output current is. All we can say is that theoretically there will be no effect from closing the switch, but that in real life there will be some degree of dimming when the switch is closed.
What would happen if a wire having no resistance at all (0 Ω) were connected directly across the terminals of a 6-volt battery? How much current would result, according to Ohm’s Law?

| |
Suppose we were to short-circuit a 6-volt battery in the manner just described and measure 8 amps of current. Why don’t the calculated figures from the previous paragraph agree with the actual measurement?
Ohm’s Law would suggest an infinite current (current = voltage divided by zero resistance). Yet, the experiment described yields only a modest amount of current.
If you think that the wire used in the experiment is not resistance-less (i.e. it does have resistance), and that this accounts for the disparity between the predicted and measured amounts of current, you are partially correct. Realistically, a small piece of wire such as that used in the experiment will have a few tenths of an ohm of resistance. However, if you re-calculate current with a wire resistance of 0.1 Ω, you will still find a large disparity between your prediction and the actual measured current in this short-circuit.
Follow-up question #1: explain why wire resistance alone does not explain the modest short-circuit current.
Follow-up question #2: identify at least one safety hazard associated with a real experiment such as this.
Remind students that short-circuit testing of electrical power sources can be dangerous. A student of mine once stuffed a 6-volt “lantern” battery in his tool pouch, only to have it discharge smoke an hour later, after the battery terminals had been shorted together by a wrench handle!
No, Ohm’s Law is not being cheated here: shorting a voltage source with a 0 Ω conductor will not result in infinite current, because there are other sources of resistance in such a circuit. The task here is to determine where those sources might be, and how they could be located.
Published under the terms and conditions of the Creative Commons Attribution License

In Partnership with Geehy Semiconductor



by Duane Benson

by Aaron Carman
The questions are very interesting.