Peak Voltage Calculator
The peak voltage calculator calculates peak voltage values from the peak-to-peak voltage, RMS voltage, or average voltage.
Output
Overview
The peak voltage calculator calculates the peak voltage value from either the peak-to-peak voltage, the RMS voltage, or the average voltage. It calculates the peak voltage based on the formulas below for each, respectively.
Equations
$$V_{P} = \frac{1}{2}*V_{P} = 0.5*V_{P}$$
$$V_{P} = \sqrt{2}*V_{rms} = 1.414*V_{rms}$$
$$V_{P} = \frac{\pi}{2}*V_{avg} = 1.571*V_{avg}$$
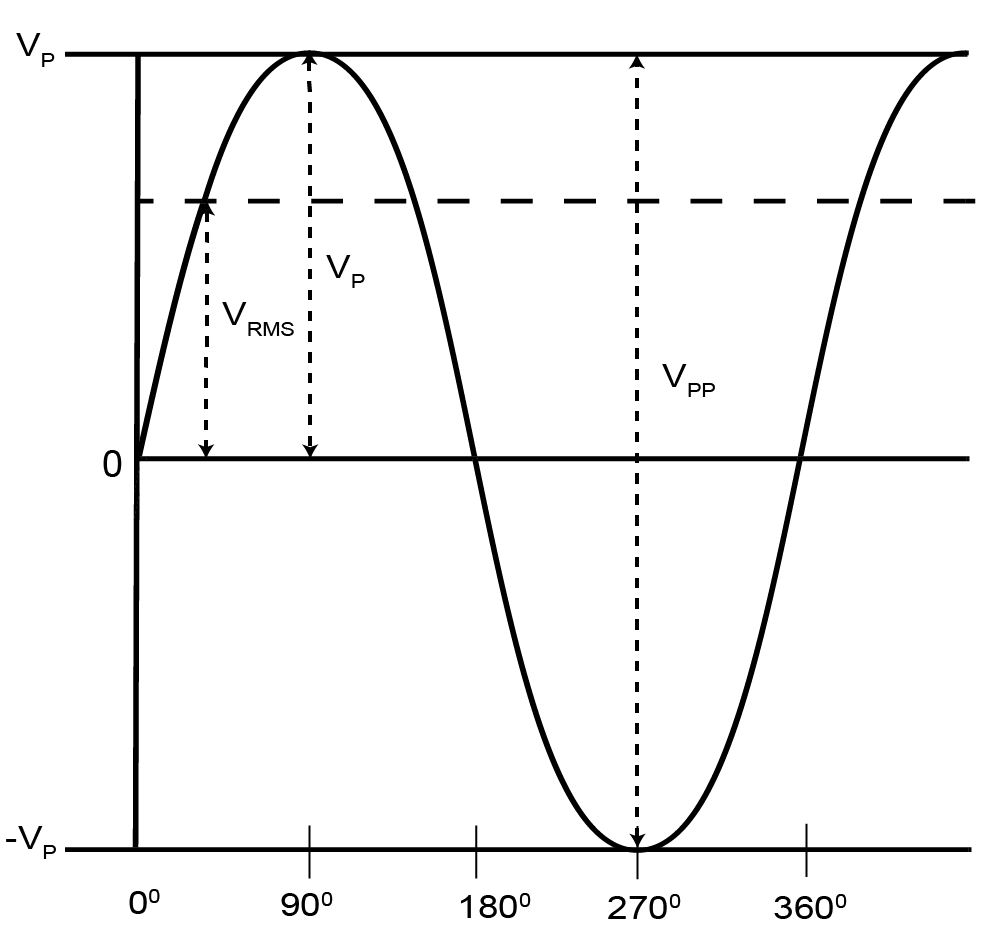
$$V_{P}$$: The maximum instantaneous value of a function as measured from the zero-volt level. For the waveform shown above, the peak amplitude and peak value are the same, since the average value of the function is zero volts.
$$V_{P-P}$$: The full voltage between positive and negative peaks of the waveform, that is, the sum of the magnitude of the positive and negative peaks.
$$V_{rms}$$: The root-mean-square or effective value of a waveform.
$$V_{avg}$$: The level of a waveform defined by the condition that the area enclosed by the curve above this level is exactly equal to the area enclosed by the curve below this level.








The first equation has a typo, the last Vp should be Vpp.
Aside from the fact that the first equation should show Vpp for the 2nd and 3rd “Vp” as: Vp=1/2 * Vpp = 0.5 * Vpp, for completeness and clarity the 2nd formula which shows that Vp is: 1.414 * RMS, it should be shown that the RMS voltage is approximately equal to 0.7071 * Vp, and in the 3rd equation it should be shown that the average voltage is approximately 0.637 * Vp.