In a previous tutorial, we defined AC signals as voltages, currents, or numerical sequences that alternate between positive and negative values. This broad definition doesn’t apply any restrictions related to the shape of the waveform. Square waves and triangle waves, for example, can be AC signals.
However, one type of signal has a special place within the AC category. The word that we use to describe these signals is sinusoidal. You will also hear them called sine waves. A sinusoidal signal looks something like this:
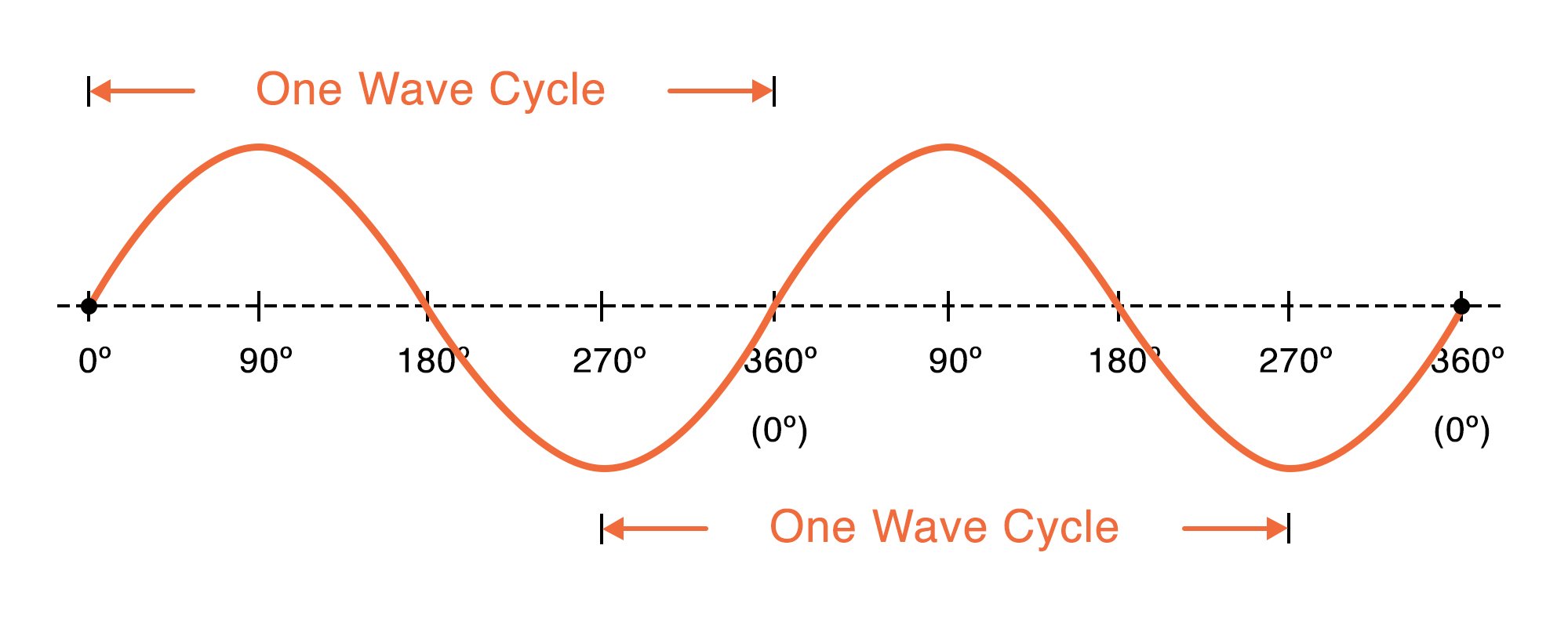
This diagram conveys some important characteristics of sinusoids:
We can mathematically generate a sinusoidal signal by means of the sine function or the cosine function. These functions operate on angles; for example, sine of 30° equals 0.5, and cosine of 0° equals 1. If we were to calculate sine values for numerous angles within a range of 0° to 360°, we would produce a sequence of numbers that, when plotted, looks like the sinusoid shown in the diagram above. If we do this with cosine instead of sine, the curve will have the same sinusoidal shape, but the initial value will be different. The following plot clarifies the difference between a sine wave and a cosine wave.

All sinusoidal signals have the same general shape, but they are not identical. The three characteristics that separate one sinusoid from another are amplitude, frequency, and phase.
Amplitude specifies the maximum distance between the horizontal axis and the vertical position of the waveform. A sine wave with an amplitude of 5 V, for example, has a maximum value of +5 V and a minimum value of –5 V.
Frequency tells us how quickly the sinusoid completes full cycles. This important characteristic influences the maximum rate at which a sinusoidal signal can transmit information and determines how a sinusoidal signal will be affected by circuits that include capacitors and inductors.
Phase refers to the horizontal position of a waveform with respect to one cycle. It is easier to understand in the context of phase shift or phase difference; we use these terms when describing the extent to which one signal is shifted to the left or right relative to another signal or to a theoretical reference signal. In the following diagram, the symbol θ indicates the phase shift (which can be measured in degrees) between a sinusoidal voltage signal and a sinusoidal current signal.

An unmodified expression of the type f(x) = sin(x) or f(x) = cos(x) will produce a sinusoidal waveform, but how do we account for the fact that sinusoidal voltage and current signals have different amplitudes, frequencies, and phase shifts? It turns out that all three of these characteristics can be incorporated as parameters into mathematical expressions built around sin() or cos(). This means that we can create a mathematical equivalent for the real sinusoids that we use in our circuits.
Amplitude is denoted by the letter A, frequency by f, and phase by the Greek letter ϕ (phi). The independent variable is time, denoted by t. Everything is arranged as follows:
\[f(t)=Asin(2\pi ft + \phi)\]
or
\[f(t)=Acos(2\pi ft + \phi)\]
The quantity 2πf is equal to the angular frequency, which is denoted by the Greek letter ω (omega). Thus, you will often see these expressions written as follows:
\[f(t)=Asin(\omega t + \phi)\]
or
\[f(t)=Acos(\omega t + \phi)\]
We’ve covered some essential information related to sinusoidal signals. In the next video tutorial, we’ll explore how these signals are used in electrical circuits and systems.

In Partnership with Future Electronics

by Aaron Carman

by Duane Benson

by Jake Hertz

by Duane Benson